

The progress of digital audio over the author's career is examined and compared to the speedups predicted by Moore's law. Then extrapolating over the next 20 years, it is concluded that the main problem facing digital audio engineers will not be how to perform a particular manipulation on sound, but how the amount of power that will be available at that time can possibly be controlled. A number of examples will be presented of computations that were not feasible at the time they were conceived, but may well become routine with pedaflop processors.
Professional audio in the 1940s and 1950s was obsessed with tone quality or with the fidelity of reproduction. The putative goal was to render as accurate a reproduction of a concert performance as possible. At the current time, we have moved beyond realistic recordings to what we might term "supernatural" recordings, that is, recordings that are so perfect that they could not have been produced in nature. Classical albums are judiciously edited, sometimes note by note, so that the performance is perfect. Our standards for recorded music are now amazingly high. Studio albums are now totally synthetic, with mixes of sounds that never could have occurred in nature. The boundary between a "real" instrument and a "synthetic" instrument, which was so clear in the 1950s, is now a continuum. Today any keyboard instrument has a library of sounds, many of which have never touched an air molecule on the way to the sample memory. We routinely subject our musical material to volumes of signal processing that would have been inconceivable in the 1950s. What can we expect in the next few decades? I will attempt to answer the question by examining equipment I used and work I did 20 years ago, and use this as a starting point to extrapolate another 20 years from now.
MOORE'S LAW APPLIED TO AUDIO
The relentless progress of technology over the last 30 years or so is nothing less then phenomenal. If the next 20 years continues at anywhere near the same rate, it will raise some interesting questions about what audio engineers will be doing by then. We have spent tremendous amounts of time shaving a few instructions out of a processing loop just to get, say, one more channel of audio through a particular processor, or one more filter in the program chain. What will happen when we don't have to do that any more? What will we spend our time doing? Although I don't claim any particular insight into the answers to these questions, I do have some experience with techniques in audio processing that are potentially useful but have previously been considered so outrageously consumptive of compute power that they were considered to be little more than intellectual curiosities.
ABOUT MOORE'S LAW
When Gordon Moore of Intel made his observation that semiconductor performance doubles every 18 months, he was talking only about the number of transistors that fit in a given area of silicon. He was not talking, for instance, about the clock rate of microprocessors, or the density of storage on hard disk drives, or network bandwidth. Each technology has its own rate of growth. They are not always the same. It is interesting to compare the rates of growth of the various technologies and compare them to Moore's law.
The demise of Moore's law continues to be greatly overrated. Some people predict the end of the increase of integrated-circuit density within the next 10 years, and others say it is more than 30 years off. This discussion reminds me a bit of the science textbook I had in the mid-1950s, which calmly noted that the world's oil supply would be exhausted by 1964. Researchers are now examining—by using quantum effects for computing elements--those same elements that were to place lower bounds on the size of transistors. Effectively, as the gate widths of transistors decrease, the leakage current due to quantum tunneling increases, and eventually the transistor stops working. This assumes that we continue to make transistors in the same way. Who can say that we won't invent a "quantum transistor," which makes specific use of quantum effects for its operation?
Other technologies, such as hard disk drives, are nowhere near the theoretical limits of their performance. The introduction of magnetoresistive (MR) heads a few years ago led to another factor of 100 or so in the bit density. The problems of decreasing signal strength from the heads fighting with increasing actuator power levels have been solved one by one and continue to be improved. Who can forget IBM's announcement of a quarter-sized hard drive storing hundreds of megabytes of data?
With this preparation, I will take some examples that I personally performed as benchmarks to the progress of technology and see where they lead us.
RAW COMPUTE POWER ON THE RISE
In 1978 I did a study of digital reverberation algorithms (Moorer 1979). I took a "shotgun" approach to the problem, which led me into a number of areas. One was to come up with a number of new unit reverberators, some of which have proved useful and some of which have not. Another was to engage in some explorations of room modeling using image sources. And finally, I examined the impulse responses of a number of real concert halls. After staring at impulse responses, both real and synthetic, for what seemed like forever, I decided that I could do just as well by using random numbers. Curiously enough, this worked quite well. I synthesized impulse responses for left and right channels by producing a sequence of 100,000 or so random numbers, then applied an exponential weighting to give the desired reverberation time. Direct convolution with these impulse responses gave what I immodestly call "the world's greatest artificial reverberation." At the time I did this experiment, it took about 10 hours of computer time for every second of audio on a DEC PDP-10. I recently tried the experiment again with my Macintosh G3. It takes about 2 seconds of computer time for every second of audio, a ratio of 18,000:1. This means that the ratio over the past 22 years is about a factor of 1.5 per year, or about 2.25 every 2 years. This is just about exactly Moore's law.
Actually, that result needs some further explanation. If we just look at the difference in actual processor speed, it is not that great. A hand-coded fast Fourier transform (FFT) routine for the same PDP-10 took about 6 Nlog2N microseconds, whereas a C-coded (unoptimized) routine takes about 1/5 Nlog2N microseconds on the G3. Part of the disparity is that the FFT routine in C could be speeded up tremendously by hand optimization. The current batch of compilers is just not up to the task with modern pipelined superscaler processors. The PowerPC 750 chip is fully pipelined, and can start a number of operations on every clock tick, but the code generators in most compilers are not prepared to take advantage of this. What, then, accounts for the increase in speed over the PDP-10 that is so disproportionate to the basic processor speed? The difference is also in memory access time. In doing this task on the G3, I used million-point FFTs, since I have 256 Mbytes of main memory. In the PDP-10, I had to break all the FFTs down into 32K units, which meant an elaborate system of paging in bits of sound and summing the results of a number of FFTs at a time to get the final output signal.
Now consider for one second what it means if the next 22 years gives anywhere near the same speedup as the previous 22 years has given. That would imply that we should be able to process 9000 channels of sound in real time, doing million-point FFTs (Fig. 1). Even the most intensive professional audio user cannot get a grip on 9000 channels—or even 900 channels. This is compute power far beyond what even the most starry-eyed fortuneteller could have imagined! It will change the very nature of what audio is, and what audio engineers do, since it changes what is possible at a fundamental level. Processes that were considered unfeasible because they were grotesquely complex will become matter-of-fact. Techniques that we abandoned decades ago will be revived and will give us power to manipulate the sound in ways that were considered impossible. I firmly believe that in 20 years, the fundamental problem facing audio engineers will not be how to accomplish a particular manipulation of the sound, but how we can possibly package this power into an environment that a human being can be expected to learn to use. If a modern mixing console can have 2000 or more controls on it, what does it mean to have a digital audio workstation that has 2 million virtual sliders and buttons? Worse yet, most of those controls will be connected to parameters that are so obscure that it requires a Ph.D. just to understand what it is you are controlling. I think the only viable solution to the issue of control will be the rise of "intelligent assistants." This idea will be discussed a bit more later.
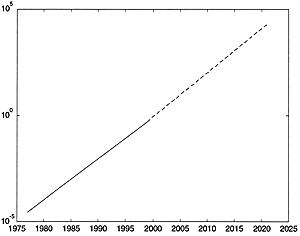 |
Fig. 1. Number of channels of million-point direct convolution that can be performed by computers the author had access to. The first two data points are a DEC PDP-10 (10 hours of compute time for every second of sound) in 1977 and a Macintosh G3 (2 seconds of compute time for every second of sound) in 1999. If we extrapolate through another 22 years, we can expect something like 9000 channels of real-time million-point direct convolution to be possible on desktop computers. |
THE GROWTH RATE OF NETWORKS
As noted, one cannot necessarily assume that other technologies increase at the same rate as semiconductor density. Curiously enough, the one technology that seems to advance faster than Moore's law would suggest is networking capacity. Local-area networks have moved from 1 Mbit per second to 10 Mbits, to 100 Mbits, and to 1 Gbit per second over this same 22-year period. That is a factor of about 1.36 per year. Although this is the basic data rate, the total networking capacity in the world has increased by even greater amounts. Bandwidth into the home over this period has moved from 300 baud to 56K over standard connections, but is measured in multiples of 100K baud when we start talking about DSL connections. This is again a factor of about 1.36 per year (Fig. 2 and 3). Curiously enough, if you extrapolate this through the next 22 years, you might guess that network connections of, say, 300 Mbaud would be available in the home. This is significantly less than the rate of increase in total network speed and capacity in the world. It would not be unreasonable to expect that the bandwidth in the home would catch up with the general rate of increase at some point. This implies that we may see a quantum jump in the capacity available to the home, which is not unreasonable since it would correspond to rebuilding the infrastructure. This is something that either happens in your area or it doesn't: you cannot send half a fiber-optic cable into your house— it is either all or none.
Lest anyone think that this level of infrastructure overhaul is too large for anyone to attempt, I remind you that two different large-scale infrastructures have been built over the last 10 years: the first is the networks (there are three) of satellite telephone systems and the other is the networks of cellular phones, which have grown like dandelions along every highway in the country. It is not out of the question at all that new fiber lines will be dragged into each and every home.
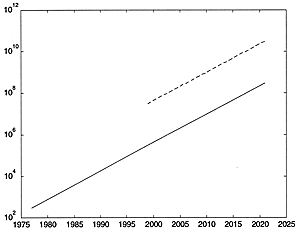 |
Fig. 2. Modem speeds, starting with 300 baud in 1977 to 300,000 baud (DSL) in 1999. An extrapolation to 2021 predicts 300 megabaud. This is at odds with the known rate of increase of network speeds and capacity in common carriers. It is not out of the question that bandwidth into the home will incur a quantum jump sometime over the next 20 years to the higher dashed line. |
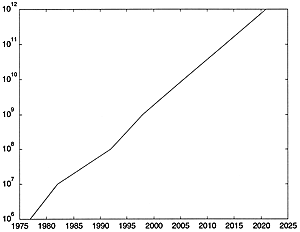 |
Fig. 3. Local-area network speeds. In 1977, Ethernet I had a speed of 1 Mbit/second, followed shortly by Ethernet II at 10 Mbits/second and 100-base-T at 100 Mbits/second. Today fiber channels allow rates of up to 1 Gbit/second. If we extrapolate this over 22 more years, we can expect LANs hitting speeds of 1 Tbit/second. The disparity between this graph and the previous one hints again at the possibility of a quantum leap in bandwidth available in the home over the next 20 years. |
If we take as a given that we can expect over the next 20 years that homes in industrialized countries will be connected by fiber-optic lines, capable of delivering gigahertz connections into every home, with multigigahertz connections to professional and commercial sites, some interesting questions arise. It leads us to the possibility that it is not out of the question that all broadcasts (radio, TV) may be formatted as IP packets. Rather than having a difference between the way digital video is transmitted between cable and Internet, we may have a convergence so that all audio and video is distributed the same way, and through the same network. You will not have separate cable TV, Internet, and telephone connections. They may all be distributed through the same format, which will be more closely related to the Internet than it is to cable TV. In the home or office, it is perfectly straightforward to listen to any number of international radio broadcasts over the net. Will this be the future of radio for fixed-position receivers? In the area where I live there is now only one remaining classical music station. It is possible that soon there will be none, in which case I will have no alternative but to connect to the net and look for classical music broadcasts. When any appliance in the house has an IP address and can connect (wirelessly?) to the dedicated lines that will run into each household, there is no reason why the boom-box of the future wouldn't have one dial for radio frequencies (since you still need local news, such as traffic reports) and one for IP addresses of broadcast stations. The real question is whether video will also be broadcast in this manner.
As for music distribution, no one can deny the advantage of inventory-free web stores. By that time the flash memories will store tens of gigabytes of data, so there will be little reason to use moving media, such as optical discs. Similarly, data compression in audio is a temporary aberration that will be swept away with time. Video may always carry some amount of compression, but you can be sure that the current compression ratios are not permanent features of the landscape.
TOM STOCKHAM AS PROPHET
I attended the Audio Engineering Society Convention in Hamburg in 1978, where Tom Stockham gave a talk on digital audio to a skeptical audience. Remember that digital audio recording devices were not commercially available. Both the Sony 1600 and the F1 were to come later. He said that by the turn of the century, we would have a device of size less than a cubic foot that would be able to record 16 channels of audio for 40 days and 40 nights. This prediction was met with an audible gasp from the audience. Let us check that prognostication.
He would have been referring to 16-bit audio at about 50-kHz sampling rate. That amounts to 100K bytes per second per channel. Thus the amount of data would be 40x24x3600x16x100K. This amounts to 5.5296 Tbytes. Using the modern 33-Gbyte drives, this would be 168 disk drives. Such a drive has a volume of about 1/36 cubic foot; so 168 drives would have a volume of about 4.5 cubic feet. Well, it appears that he missed the mark a bit, but not by a lot. If we add some space for ventilation and cabling, such a storage unit would easily fit in a standard 6-foot-tall 19-inch rack. If we extrapolate another 20 years, using the same ratio, we will be using 200-Tbyte drives on our personal computers (Fig. 4). A typical professional system might have several pedabytes of total storage. If we take our basic unit of "standard" audio to be 192-kHz, 24-bit, 256-channel audio, this means that a single 200-Tbyte drive will handle about 14 days and 14 nights of audio. If this sounds a bit silly, let me remind everyone that there are reasons (discussed later) to use hundreds of microphones in live recording situations, since this gets us increasingly close to obtaining enough information to recreate the wave front itself.
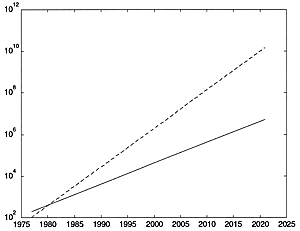 |
Fig. 4. Increase in hard-disk storage capacity. The lower (solid) line shows the capacity from the 200-Mbyte storage-module drives in 1977 to the 33-GB drives available today. Extrapolated to 2021, this would imply that we would have 2.7 Tbyte drives available. If you take size into account as well, you get the upper (dashed) line. The upper line is in megabytes per cubic foot. Note that the storage module drive was about 2 cubic feet, whereas the 33-GB drive is only about 1/36 of a cubic foot. This implies that in 2021, in 1/36 of a cubic foot, we should be able to get 380-Tbyte drives. Alternately, the 2.7-Tbyte drives will be so small that they might be attached directly to the motherboard. |
WHO IS THE TAIL AND WHO IS THE DOG?
The fact that the professional audio industry uses technology from the computer industry leads some luminaries to conclude that audio benefits passively from the march of technology. This was true in the 1950s and 1960s, but started to change in the 1970s. Let us not forget some of the technologies that were originally developed entirely for the consumer entertainment industry (some of them are video rather than audio) and that are now indispensable parts of modern computers (or are obsolete).
I might also point out that the most elaborate computing engines in the home right now are the latest 128256-bit video engines in video games. The upcoming Sony Emotion Engine for the PlayStation II is said to sport 42 million transistors. This is several times larger than any CPU chip on the market in this time frame. These are tremendously complex SIMD graphics engines, which stretch the limits of semiconductor manufacture. Mainstream computer chips are now being delivered with SIMD array processor subsections (Intel MMX, Motorola AltiVec) that used to be the exclusive domain of large-scale government research projects, such as weather simulation or simulation of nuclear weapon explosions. Clearly, these features have no application whatsoever in word processing or spreadsheets. They are strictly for entertainment value. I will make an assertion that rather than the entertainment industry being driven by the semiconductor industry, we are seeing more and more features being incorporated into the desktop PC which either are derived from the entertainment industry or are developed specifically for entertainment value. In this kind of progress it is the techniques and discoveries from the professional industry that gradually become accepted into the consumer markets. It is what we do today in the studios that will determine what will be seen in the home in the next 20 years.
HOW WILL THIS POWER AFFECT PROFESSIONAL AUDIO?
I will now move beyond things I have actually seen or done into areas that will be technologically possible and are not in use today. Whether these particular ideas turn out to be useful or not is unknowable at this time, but these are areas that I know are interesting and can be useful. I hope that these will serve as a starting point for further discussion and research.
WHERE WAS IT?
In 20 years loudspeakers and microphones will know where they are. I can suggest some ways that this can be accomplished; we have the technology today. One simple way for loudspeakers to locate themselves would be for each to emit a series of tone bursts. Then, using triangulation with four or more loudspeakers, the location (including elevation) of all the loudspeakers can be determined. Note that for this to work, each loudspeaker has to have a microphone in it to pick up the tone bursts from the others. For loudspeakers that have a permanent magnet in them, this is already built in. Any permanent-magnet loudspeaker is a dynamic microphone—not a very good one, but good enough to allow you to locate the loudspeakers. We might also envision loudspeakers and microphones with tiny GPS receivers in them, since the accuracy of GPS will be improved by then, and GPS receivers will cost nothing and will find their way into just about everything, such as cell phones, wrist watches, maybe even small children. Now what does this do for us?
Consider recording a symphony orchestra. You might have 100 musicians involved. If you have more microphones than sound sources, then the redundant information can be used to "sharpen" the directionality of the microphones. If the number of microphones is several times the number of musicians, and if they are placed relatively close to the musicians, then we can use noise-cancellation techniques (Widrow and Stearns, 1985) to produce the sound of each instrument on a separate channel, with the sound of the rest of the orchestra attenuated. Although it is not strictly necessary to know the locations of the microphones, or the locations of the musicians, the process can be made more accurate with this additional information.
Needless to say, there is no way that we can continue to use the infamous microphone "snake" when we talk about hundreds of microphones. They will have to communicate wirelessly and connect together into a seamless network, each with its own IP address. They will have to contain their own analog-to-digital converters and network interface. Presumably they must also accept commands to do things such as adjust the gain or perhaps the pickup pattern (assuming we are still using pressure-gradient microphones by then).
THE JOYS OF SUPERSAMPLING
The last year of the millennium saw the wide acceptance in the professional audio world of sampling rates capable of carrying information significantly beyond the range of human hearing. Although this has been met with some (deserved) amount of skepticism, there are good technical reasons for using an even higher sampling rate during the production chain. Sampling rates of 8x48k, 16x48k, or even 32x48k have certain advantages in production. Although these advantages are most evident in nonlinear processing, such as dynamics and signal reconstruction, they exist for linear operations as well.
It is well known that nonlinear operations produce unwanted sidebands. Often these sidebands exceed the Nyquist rate and are consequently folded into audible frequency ranges. One nonlinear operation that is considered important is time-base correction by frequency-domain manipulations (Moorer 1978, Laroche and Dolson 1999, Quatieri and McAulay 1985). It involves computing the magnitude and phase of the short-term Fourier transform of the signal, then producing a new sequence of transforms by interpolating the magnitude and rotating the phases before taking the inverse Fourier transform. This involves two nonlinear operations (taking the magnitude and extracting the phase by arctangent) and a manipulation on the resulting values. Any manipulation of these values can be expected to produce sidebands. Two kinds of aliasing can result if care is not taken in the process. There can be frequency aliasing, where unwanted sidebands are folded into the audible range. There can also be time aliasing, where the resulting signal would be longer than the number of time points in the transform and would consequently be folded back into the other end of the time window. This produces the familiar echo or reverberation, which so often results from this kind of process.
The frequency aliasing is easily fixed with supersampling. Since we can safely assume that we start with no significant signal energy above, say, 300 kHz, we can window the resulting spectrum in the frequency domain to eliminate the unwanted sidebands. The time aliasing can be ameliorated by padding the data before transforming with zeros. With unlimited compute power at our disposal, padding ratios of 16:1, 32:1, or higher can be contemplated. To make use of this extra information, we have to approximate the nonlinear operation with a linear operation. This can be done by taking the ratio of the previous transform and the current transform (which was produced by nonlinear operations such as rotating phases or interpolating magnitudes) and identifying that ratio as the transfer function of a linear filter. We can then take the inverse transform of this filter and window it in the time domain to produce an approximation that will not produce time aliasing. Clearly, the larger the transform, the more accurate this approximation can be.
HIGH-ORDER LINEAR PREDICTION
In the mid-1970s I pioneered a technique combining linear prediction with the phase vocoder (Moorer, 1979 Mar.). I used what seemed like relatively high-order linear prediction (35th order at a 25-kHz sampling rate) to compute the residual of a piece of vocal music, Then I used the phase vocoder to shift the pitch of the residual, and I reapplied the spectral envelope with the filter determined by the linear-prediction step. This produces what might be called the "ultimate" sampling synthesizer: it smoothly shifts the pitch of a signal without any change to the timbre or vowel quality. Fig. 5 shows the data flow of the process. First a high-order linear predictor is used to strip the spectral envelope off the signal. Then time or frequency modifications can be performed in any number of ways (phase vocoder per Moorer 1978 and Laroch and Dolson 1999; MQ analysis/synthesis per Quatieri and McAulay 1985; time-domain microediting). The spectral envelope may then be reapplied in either unmodified or modified form. All-pass transformations may be used to transform the final synthesis filter if changes to the timbre (vowel quality) are desired.
With lower sampling rates, such as 48 kHz, the all-pass modification provides a nonlinear spectral warping. With oversampling by factors of 4 or 8, the spectral warp in the audible band becomes very linear. This technique does have some problems that have to be resolved. For instance, in normal sound (such as human speech) there are certain spectral areas that have very little energy, and can thus be considered to be noise. If you pitch-shift the residual, those spectral regions get moved around. They can end up underneath a powerful spectral peak. This can result in amplifying the noise in that spectral region to an audible region. Some modifications to some signals will produce undesirable artifacts. There are probably solutions to this issue.
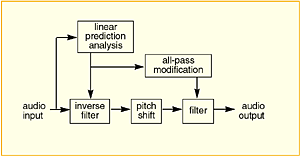 |
Fig. 5. Use of high-order linear prediction for the modification of signals without disturbing the spectral envelope, or for independent modification of pitch and spectral envelope. For pitch modification alone, no all-pass modification of the prediction filter is necessary. Pitch shifting can be performed by phase vocoder, by MQ analysis or synthesis, by time-domain microediting, or by any other technique. Performing this on the residual rather than the original signal ensures that the spectral envelope can be reimposed without alteration. Alternately, no pitch shifting need be performed, and the all-pass spectral envelope modification can be used to change the timbre (vowel quality) of the sound. |
"RUNNING" TRANSFORMS
Transform-based computations are generally made by "hopping" the transform forward in time by some number of samples, such as by half the window length. There is some advantage to be gained by computing the transform at every sample. This has generally been considered to be computationally prohibitive, but it won't always be that way. It is interesting to note that a running transform can be performed with only N operations per point as follows (Moorer 1984). First we take the definition of an N-point discrete Fourier transform:
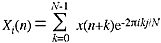
It is a simple matter of writing out the summation to derive the following relation:
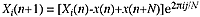
This gives us a full transform at every point of the signal. The complex rotation is numerically very stable, so this process can be expected to give good results over millions of points by using 64-bit floating-point arithmetic.
One might object that we have provided no windowing of the input signal. This can be done in the frequency domain, but some care must be taken to get reasonable results. For instance, the standard Hamming window may be applied by combining groups of three frequency values as follows:
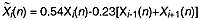
Any window that can be represented by a limited sum of cosines can be easily realized in this manner. This class of windows includes Hamming, Hanning, Blackman, and many others (Moorer 1986, Rife and Vincent 1970).
As noted, it is sometimes important to take a transform length that is many times larger than the data length so that a finely interpolated spectrum is obtai
